Further analysis of the symbolics.
What if we assigned a different meaning to the words "left" and "right", keeping the formulae but forgetting about paths. What else could it mean?
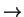"left out", "right"
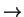"stay right
there".
Given a set of objects, The combination formula tells us how many
subsets of a
certain size there are. The some of these answers is the total number of
subsets. What is the sum of the numbers in Row n of the triangle? It's
the number of possible subsets of a set of n objects. It's 2n, since
each element of the set can be "left out" or "stay right there", two
choices for each element.
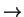0, "right"
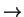1: binary numbers,
each spot is a power
of 2. We have a 1's place, a 2's place, a 4's place, etc., just
like 1's, 10's, and 100's in "normal" numbers. Every "path of left
and rights" can be matched to a string of 0's and 1's that can be
matched to a "binary number". We have a "more natural" number system for
numbering paths than the clunky base ten. When would base 10 be better?
If there were 10 choices instead of 2 at each turn. That triangle would
be a mess to draw, though. But it would be not so bad for base 1 or base
3. Try these at home for homework. Draw an "alternate Pascal's
triangle", where each point in the triangle is connected to 3 points
above and 3 points below.
More on this (bases) in a few days.