Algebraic Exploration: Finding Patterns in Triangle

Numeric patterns in the triangle: compare combinatoric and geometric proofs. Left-right (reflective) symmetry in the triangle corresponds to subsstitution symmetry in the combinatoric formula from Day 6. $(m) \leftrightarrow (n-m)$ is the algebraic expression for of horizontally reflecting the triangle.

$$\frac{n!}{m!(n-m)!} = \frac{n!}{(n-m)!m!} =\frac{n!}{(n-m)!((n-(n-m))!}$$

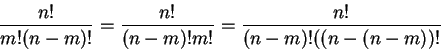
Prove "The sum of the squares of the numbers in row n" equals "the number in the middle of row n" and other theorems.